
Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


Problemario preparación Exámen a Título
Agosto 20111 El valor p es 3.141592654... ¿Cuál es su valor con 4 cifras significativas?
2 ¿Cuál es el valor e (la base de los logaritmos naturales) con 5 cifras significativas?
3 Determine el valor de la expresión 1/(2 - p) con 3 cifras significativas.
4 Si x = 3, ¿cuál es el valor de la expresión 1 - e-x con 3 cifras significativas?
5 Suponga que acaba de comprar un Ferrari Dino 246GT y quiere saber si puede usar su juego de llaves SAE (unidades del sistema inglés) para trabajar en él. Usted tiene llaves con anchos w = 1/4 pulg, 1/2 pulg, 3/4 pulg y 1 pulg, y el auto tiene tuercas con dimensiones n = 5 mm, 10 mm, 15 mm, 20 mm y 25 mm. Si definimos que una llave ajusta si w no es 2% mayor que n , ¿Cuál de sus llaves puede usar?

6 La locomotora Rocket de 1829 podía jalar un carro con 30 pasajeros a 25 mill/hora. Determine su velocidad con tres cifras significativas, en km/h.
7 Los “trenes bala” de alta velocidad comenzaron a correr entre Tokyo y Osaka en 1964. Si un tren bala viaja a 240 km/h, ¿cuál es su velocidad en mi/h con tres cifras significativas?

8 Los ingenieros que estudian ondas de choque suelen expresar la velocidad en milímetros por microsegundo (mm/ms). Suponga que la velocidad de un frente de onda es de 5 mm/ms. Determine esta velocidad: (a) en m/s, (b) en mi/s.
9 Un geofísico mide el movimiento de un glacial y descubre que se está moviendo 80 mm/año. ¿Cuál es su velocidad en m/s?
10 La aceleración debida a la gravedad al nivel del mar en unidades SI es g = 9.81 m/s2. Convierta este valor a millas/s2
11 Un estadio (1 furlong = 1/8 de milla) por quincena(1 quincena=15 segundos), esto una unidad chusca de velocidad, inventada tal vez por un estudiante como comentario satírico sobre la enredada variedad de unidades con que los ingenieros tienen que tratar. Si usted camina 5 pie/s , ¿cuál es su velocidad en estadios por quincena con tres cifras significativas?
12 El área de la sección transversal de una viga es igual a 480 pulg2. ¿Cuál es el área de su sección transversal en m2?
13 Un camión puede cargar 15 yardas cúbicas de grava. (1yarda = 3 pies). ¿Cuántos metros cúbicos puede cargar?
14 Un transductor de presión mide un valor de 300 lb/pulg2. Determine el valor de la presión en pascales. Un Pascal (Pa) es igual a 1 N/m2.
15 Un caballo de fuerza equivale a 550 Ib-pie/s. Un watt equivale a 1 N-m/s. Determine el número de watts generados por
(a) el avión de los hermanos Wright (1903), que tenía un motor de 12 caballos de fuerza;
(b) un avión jet con potencia de 100 000 caballos de fuerza a velocidad de crucero.

16. Una placa rectangular tiene una longitud de (21.3 +- 0.2) cm y un ancho de (9.8 +- 0.1) cm. Calcule el área de la placa, incluyendo su incertidumbre.
17. El radio de un círculo se mide que es (10.5 +- 0.2) m. Calcule el
a) área
b) circunferencia del círculo y dé la incertidumbre en cada valor.
18. El radio de una esfera sólida se mide como (6.50 +- 0.20) cm, y su masa se mide como (1.85 +- 0.02) kg. Determine la densidad de la esfera en kilogramos por metro cúbico y la incertidumbre en la densidad.
19. Realice las siguiente operaciones aritméticas:
a) La suma de los valores medidos 756, 37.2, 0.83 y 3.5
b) El producto 0.0032 x 356.3
c) El producto 5.620 x p
20. El año tropical, el tiempo entre equinoccio primaveral al siguiente equinoccio primaveral, es la base de nuestro calendario. Contiene 365.242 199 días. Encuentre el número de segundos en un año tropical.
21. Un agricultor mide la distancia alrededor de un campo rectangular. Las longitud de los lados largos del rectángulo se encuentra que es 38.44 m, y la longitud de los lados cortos resulta ser de 19.5 m.¿Cuál es la distancia total alrededor del campo?
22. Se va a construir una banqueta alrededor de una piscina que mide (10.0 +- 0.1) m por (17.0 +- 0.1) m. Si la banqueta debe medir (1.00 +- 0.001) m de ancho por ( 9.0 +- 0.1) cm de grueso, ¿qué volúmen de concreto se necesita, y cual es la incertidumbre aproximada de este volumen?
23. En unidades del sistema SI, la constante de la gravitación universal es G = 6.67 x 10-11 N-m2/kg2. Determine el valor de G en unidades del sistema inglés.
(a) ¿Cuál es su masa en slugs?
(b) ¿Cuál es su masa en kilogramos?
(c) Un automóvil ordinario tiene una masa de aproximadamente 1000 kilogramos. ¿Cuántos automóviles se deberían tener para obtener un peso igual al del tractor al nivel del mar?
 (Ninguno de los elementos está a escala)
(Ninguno de los elementos está a escala)25. La aceleración debida a la gravedad es de 13.2 pie/s2 en Marte y de 32.2 pie/s2 en la Tierra. Si una mujer pesa 125 lb sobre la Tierra, ¿cuánto pesará en Marte?
26. La aceleración debida a la gravedad es de 13.2 pie/2 sobre la superficie de Marte y de 32.2 pie/s2 sobre la superficie de la Tierra. Una mujer pesa 125 lb en la Tierra. Para sobrevivir y trabajar en la superfice de Marte, debe portar un traje y un equipo especiales, así como herramientas. ¿Cuál es el peso máximo admisible en la Tierra de la ropa, el equipo y las herramientas de la astronauta si los ingenieros no quieren que en Marte el peso total rebase las 125 libras?
27. Una persona tiene una masa de 50 kg.
(a) La aceleración debida a la gravedad al nivel del mar es g = 9.81 m/s2. ¿Cuál es el peso de la persona al nivel del mar?
(b) La aceleración debida a la gravedad en la superficie de la Luna es de 1.62 m/s2. ¿Cuál sería el peso de la persona en la Luna?
28. La aceleración debida a la gravedad al nivel del mar es g = 9.81 m/s2. El radio de la Tierra es de 6370 km. La constante gravitatoria universal es G = 6.67 por 10-11 N-m2/kg2.
Use esta información para determinar la masa de la Tierra.
29. Una persona pesa 180 lb al nivel del mar. El radio de la Tierra es de 3960 millas. ¿Qué fuerza ejerce la atracción gravitatoria de la Tierra sobre la persona si ésta se encuentra en una estación espacial en órbita a 200 millas de la Tierra?
30. La aceleración debida a la gravedad en la superficie de la Luna es de 1.62 m/s2. El radio de la Luna es RM, = 1738 km. Determine la aceleración debida a la gravedad en la Luna en un punto ubicado 1738 km arriba de su superficie.
31. Si un cuerpo está cerca de la superficie de la Tierra, la variación de su peso con la distancia desde el centro de la Tierra con frecuencia puede despreciarse. La aceleración debida a la gravedad al nivel del mar es g = 9.81 m/s2. El radio de la Tierra es de 6370 km. El peso de un cuerpo al nivel del mar es mg, donde m es su masa. ¿A qué altura sobre la superficie de la Tierra el peso del cuerpo se reduce a 0.99 mg?
32. Los centros de dos naranjas se encuentran a un metro de distancia. La masa de cada naranja es de 0.2 kg. ¿Qué fuerza gravitatoria ejercen entre sí las naranjas? (La constante gravitatoria universal es G = 6.67 x 10-11 Nm2/kg2.)
33. Una pulgada es igual a 25.4 milímetros. La masa de un metro cúbico de agua es de 1000 kilogramos. La aceleración debida a la gravedad al nivel del mar es g = 9.81 m/s2. El peso de un pie cúbico de agua al nivel del mar es aproximadamente igual a 62.4 lb. Usando esta información, determine a cuántos newtons equivale una libra.
34. La gráfica de la posición s de un punto en función del tiempo es una línea recta. Cuando t = 4 s, s = 24 m, y cuando t = 20 s, s = 72 m.
(a) Determine la velocidad del punto calculando la pendiente de la línea recta.
(b) Obtenga la ecuación para s en función del tiempo y úsela para determinar la velocidad del punto.
35. La gráfica de la posición s de un punto de una fresadora en función del tiempo es una línea recta. Cuando t = 0.2 s, s = 90 mm. Durante el intervalo de tiempo de t = 0.6 s a t = 1.2 s, el desplazamiento del punto es Ds = -180 mm.
(a) Determine la ecuación para s en función del tiempo.
(b) ¿Cuál es la velocidad del punto?
36. La gráfica de la velocidad v de un punto en función del tiempo es una línea recta. Cuando t = 2 s, v = 4 pie/s, y cuando t = 4 s, v = -10 pie/s.
(a) Determine la aceleración del punto calculando la pendiente de la línea recta.
(b) Obtenga la ecuación para v en función del tiempo y úsela para determinar la aceleración del punto.
37. La posición de un punto está dada por s = 2t2 - 10 pie.
(a) ¿Cuál es el desplazamiento del punto entre t = 0 y t = 4 s?
(b) ¿Cuáles son la velocidad y la aceleración en t = O?
(c) ¿Cuáles son la velocidad y la aceleración en t = 4 s?
37. Describa el campo vectorial F = 2y i - 2xj, eligiendo por lo menos cuatro puntos en el plano cartesiano (uno en cada cuadrante).
38.Un cohete consta de una carga útil de 5Mg y un impulsor de 50Mg. El 80% de la masa del impulsor es combustible y su velocidad de escape es de 1.5 km/s. Si el cohete parte del reposo y se ignoran las fuerzas externas, ¿qué velocidad alcanzará?
38. Un cohete parte del reposo y viaja hacia arriba en línea recta. Su altura sobre el suelo se mide con un radar desde t = 0 hasta t = 4 s, y se puede expresar de manera aproximada por medio de la función s = 10t2 m.
(a) ¿Cuál es el desplazamiento durante este intervalo de tiempo?
(b) ¿Cuál es la velocidad en t = 4 s?
(c) ¿Cuál es la aceleración durante los primeros 4 s?
39,Un cohete tiene una masa inicial de 3500 toneladas y una masa final de 2980 toneladas después de haber quemado el combustible. Los gases son expulsados a razón de 1587.6 kg/s.
La velocidad de escape es de 75000 ms-1. Vo es igual a 0 ms-1
Encuentre la máxima velocidad de esta etapa del cohete tomando en cuenta la acción de la gravedad.
39. La posición de un punto durante el intervalo de tiempo de t = 0 a t = 6 s es s = - 1/2t3 + 6t2 + 4t m.
(a) ¿Cuál es el desplazamiento del punto durante este intervalo de tiempo?
(b) ¿Cuál es la velocidad máxima durante este intervalo de tiempo, y en qué momento ocurre?
(c) ¿Cuál es la aceleración cuando la velocidad es máxima?
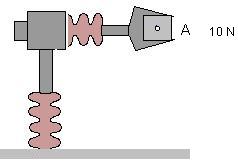
39.El robot de la figura está programado de tal manera que x=4 + t2 cm , y= 1/4 x2 cm, z=0
durante el intervalo de tiempo t=0 a t= 4s. Determinar:
a) Las componentes x y y de la fuerza total ejercida por llas tenazas del robot sobre la pieza A, en Newtons, a los 2 segundos.
b) La posición de la pieza en centimetros, cada 0.1 segundos hasta los 4 segundos
c) La magnitud de la fuerza ejercida por las tenazas sobre la pieza A a los 3 segundos.
40.Un cuerpo cuya masa es de 2 kg está sujeta a una fuerza F=(100t + 10)N, se mueve en línea recta.
En el tiempo t=0, el cuerpo está en x0=4 m con una velocidad v0= 9 m/s. Encuentre la posición del cuerpo en cualquier tiempo.
40. La posición de un punto durante el intervalo de tiempo de t = 0 a t = 3 s es s = 12 + 5t2 - t3 pie.
(a) ¿Cuál es la velocidad máxima durante este intervalo de tiempo, y en qué momento ocurre?
(b) ¿Cuál es la aceleración cuando la velocidad es máxima?
40.El vector posición de un cuerpo de masa 6 kg es r = (3t 2 – 6 t) i - 4t3 j + (3t+ 2)k metros. Determinar:
a) La fuerza que actúa sobre la partícula
b) El torque con respecto al origen que actúa sobre la partícula
41. Un sismógrafo mide el movimiento horizontal del terreno durante un sismo. Al analizar los datos, un ingeniero determina que para un intervalo de 10 segundos comenzando en t = 0, la posición se puede expresar aproximadamente con s = 100 cos(2pf) mm. ¿Cuáles son
(a) la velocidad máxima y
(b) la aceleración máxima del terreno durante el intervalo de 10 segundos?
42. Durante una operación de ensamblaje, el brazo de un robot se mueve a lo largo de una línea recta. Durante un intervalo de tiempo de t = 0 a t = 1 s, su posición está dada por s = 3t2 - 2t3 en pulgadas. Determine, durante ese intervalo de 1 se-gundo:
(a) el desplazamiento del brazo;
(b) los valores máximo y mínimo de la velocidad;
(c) los valores máximo y mínimo de la aceleración.
43. Durante la prueba de un vehículo, el conductor parte del reposo en t = 0, acelera y luego aplica los frenos. Los ingenieros que miden la posición del vehículo encuentran que de t = 0 a t = 18 s, la posición se puede representar por medio de la relación s = 5t2 + 1/2t3 - 1/50t4.
(a) ¿Cuál es la velocidad máxima y en qué momento ocurre?
(b) ¿Cuál es la aceleración máxima y en qué momento ocurre?
43.1. El vector posición de un cuerpo de masa 6 kg es r = (3t 2 – 6 t) i - 4t3 j + (3t+ 2)k metros. Determinar:
a) La fuerza que actúa sobre la partícula
b) El torque con respecto al origen que actúa sobre la partícula
43.2Durante un vuelo de prueba, un helicóptero parte del reposo en t=0; acelerómetros montados a bordo indican que sus componentes de aceleración entre t =0 y t= 10 s están dados por:
ax= 0.6t ms-2
ay= 1.8 -0.36t ms-2
az= 0
Determine la velocidad y posición del helicóptero en función del tiempo.
44. Suponga que se quiere representar la posición de un vehículo que está siendo probado por medio de la serie de potencias s = A + Bt + Ct2 + Dt3, donde A, B, C y D son constantes.
El vehículo parte del reposo en t = 0 y s = 0. En t = 4 s, s = 176 pies, y en t = 8 s, s = 448 pies.
(a) Determine A, B, C y D.
(b) ¿Cuáles son la velocidad y la aceleración aproximadas del vehículo en t = 8 s?
45. La aceleración de un punto es a = 20t m/s2. Cuando t = 0, s = 40 m y u = -10 m/s. ¿Cuáles son la posición y la velocidad en t = 3 s?
46. La aceleración de un punto es a = 60t - 36t2 pie/s2. Cuando t = 0, s = 0 y u = 20 pie/s.
¿Cuáles son la posición y la velocidad en función del tiempo?
47. Suponga que durante el diseño preliminar de un automóvil, se considera que su aceleración máxima es aproximadamente constante.
¿Qué aceleración constante es necesaria si se quiere que el automóvil alcance desde el reposo una velocidad de 55 mi/h en 10 s?
¿Qué distancia recorrería el automóvil en ese tiempo?
48. Un entomólogo calcula que una pulga de 1 mm de longitud alcanza al saltar una velocidad de 1.3 m/s en una distancia igual a la longitud de su cuerpo.
¿Qué aceleración constante se necesita para alcanzar esa velocidad?
49. Los cohetes diseñados como defensa contra los cohetes balísticos alcanzan aceleraciones superiores a 100 g, es decir, mayores que 100 veces la aceleración de la gravedad. Si un cohete tiene una aceleración constante de 100 g,
¿cuánto tiempo tarda en alcanzar una velocidad de 60 mi/h a partir de1 reposo?
¿Cuál es su desplazamiento durante ese tiempo?
52. En 1960 R.C. Owens, jugador de los Baltimore Colts, atajó un gol de campo de los Washington Redskins saltando y desviando la pelota frente a la meta a ll pies sobre el terreno. Si él medía 6 pies 3 pulg y podía alcanzar 1 pie ll pulg sobre su cabeza, ¿qué velocidad vertical tenía al saltar?
53. La velocidad de un trineo es v = 10t pie/s. Si t = 2 s, su posición es s = 25 pie. ¿Cuál es su posición si t = 10 s?
53.El vector posición de un cuerpo de masa 6 kg es r=(3t2-6t)i –4t3j + (3t+2)k metros. Determinar la fuerza que actúa sobre el cuerpo
54. La aceleración de un cuerpo es a = 30 - 6t pie/s2. Cuando t = 0, s = 0 y v = 0.
¿Cuál es su velocidad máxima durante el intervalo de tiempo de t = 0 a t = 10 s?
55. La velocidad de un cuerpo es v = 200 - 2t2 m/s. Cuando t = 3 s, su posición es s = 600 m.
¿Cuáles son la posición y la aceleración del cuerpo en t = 6 s?
56. Se mide la aceleración de una pieza sometida a una operación de maquinado y se obtiene que a = 12 - 6t mm/s2. Cuando t = 0, u = 0. Para el intervalo de tiempo de t = 0 a t = 4 s, determine:
(a) la velocidad máxima;
(b) el desplazamiento.
57. El cohete del Prob.49. parte del reposo y acelera hacia arriba durante 3 s a 100 g. Después de 3 s, su peso y la resistencia aerodinámica le ocasionan una desaceleración casi constante de 4 g.
¿Cuánto tarda el cohete en alcanzar una altura de 50 000 pies desde el suelo?
58. Un automóvil viaja a 30 mi/h cuando se enciende la luz amarilla de un semáforo que se encuentra 295 pies adelante. La luz amarilla permanecerá 5 s antes de que se encienda la roja.
(a) ¿Qué aceleración constante permitirá que el automóvil alcance la luz en el instante en que cambie a la roja, y cuál será la velocidad del automóvil cuando llegue al semáforo?
(b) Si el conductor decide no alcanzar la luz a tiempo, ¿qué aceleración constante permitirá que el automóvil se detenga justo antes de llegar al semáforo?
59. En t = 0, un conductor que viaja a 100 km/h ve un vena do en el camino, 100 m adelante. Después de un tiempo de reac ción de 0.3 s, aplica los frenos y desacelera a una razón constante de 4 m/s2. Si el venado tarda 5 s desde t = 0 para reaccionar y abandonar el camino, ¿podrá el conductor esquivarlo?
60. Un tren de alta velocidad tiene una velocidad máxima de 100 m/s. Para comodidad de los pasajeros, la magnitud de la aceleración y desaceleración se limita a 2 m/s2.
Determine el tiempo mínimo requerido para un viaje de 100 km.
Estrategia: Un procedimiento gráfico puede ayudar a resolver este problema. Recuerde que el cambio de posición de un tiempo inicial to a un tiempo t es igual al área definida por la gráfica de la velocidad en función del tiempo de to a t.
61. La estrella más cercana a nosotros después del Sol es Alfa Centauri, que está a 4.22 años luz de la Tierra. Ignorando el movimiento relativo entre el sistema solar y Alfa Centauri, suponga que una nave espacial acelera desde la vecindad de la Tierra a 0.01 g (0.01 veces la aceleración debida a la gravedad al nivel del mar) hasta que alcanza un décimo de la velocidad de la luz, viaja por inercia hasta que llega el momento de desacelerar, luego desacelera a razón de 0.01 g hasta que llega al reposo cerca de Alfa Centauri.¿Cuánto tiempo dura el viaje? (La luz viaja a 3 X 108 m/s. Un año solar es igual a 365.2422 días solares.)
62. Un auto de carreras parte del reposo y acelera a a = 5 + 2t pie/s2 durante 10 s. Se aplican los frenos y el auto adquiere una aceleración constante a = -30 pie/s2 hasta que se detiene. Determine:
(a) la velocidad máxima;
(b) la distancia total recorrida;
(c) el tiempo total del recorrido.
63. Cuando t = 0, la posición de un punto es s = 6 m y su velocidad es v = 2 m/s. De t = 0 a t = 6 s, su aceleración es a = 2 + 2t2 m/s2. De t = 6 s hasta que alcanza el reposo, su aceleración es a = -4 m/s2.
(a) ¿Cuál es el tiempo total de viaje?
(b) ¿Qué distancia total cubre el desplazamiento?
63.Un cuerpo cuya masa es de 5 kg está sujeta a una fuerza F=(140t + 20)N, se mueve en línea recta. En el tiempo t=0, el cuerpo está en x0=5 m con una velocidad v0= 6 m/s. Encuentre la posición del cuerpo en cualquier tiempo.
64. Zoólogos que estudian la llanura Serengeti calculan que, en promedio, un guepardo adulto puede correr a 100 km/h y la gacela, en promedio, puede correr a 65 km/h. Si los animales corren a lo largo de la misma línea recta, comenzando al mismo tiempo, y ambos tienen aceleración constante y alcanzan su velocidad máxima en 4 s,
¿cuán cerca debe estar un guepardo cuando la caza comienza para dar alcance a la gacela en 15 s?
64.Tres cuerdas, localizadas en un plano vertical, están fijas en diferentes puntos sobre un techo horizontal. Los otros extremos están sostenidos en un punto A, del cual pende un peso W. Los angulos formados por las cuerdas son de 35º, 100º y 160º. Las tensiones en las primeras dos cuerdas son de 100 kgf y 75 kgf respectivamente.
Determinar la tensión en la tercera cuerda y el peso W. 65. Suponga que una persona conduce su automóvil a 15 mi/h en una zona de 55 mi/h y rebasa a una patrulla de policía que va a 55 mi/h en la misma dirección. Si la patrulla acelera hasta 80 mi/h en 4 s con aceleración constante desde el momento en que es rebasada,
¿cuánto tardará en alcanzar al auto?
65.Una persona que pesa 120 N se está sosteniendo de una barra horizontal. Determinar la fuerza que ejerce cada uno de sus brazos sobre la barra cuando:
a)Sus brazos están paralelos entre sí
b)Cada brazo forma un ángulo de 30º con la vertical
66. Si q= 1 rad y dq/dt = 1 rad/s,¿cuál es la velocidad de P respecto a O?
Estrategia: Se puede escribir la posición de P respecto a 0 como
s = (2 pie) cos q + (2 pie) cos q,
y luego calcular la derivada de esta expresión con respecto al tiempo para determinar la velocidad.
67. En el problema 66, si q = 1 rad, dq/dt = -2 rad/s y d2q/dt2 = 0,¿cuáles son la velocidad y la aceleración de P respecto a O?
68. Si q = 1 rad y dq/dt = 1 rad/s, ¿cuál es la velocidad de P relativa a O?
2.36 La aceleracion de un cuerpo es a = -2v m/s2. Cuando t = 0, s = 0 y v = 2 m/s. Determine la velocidad del cuerpo en función del tiempo.
2.37 En el Prob. 2.36, determine la posición del cuerpo en función del tiempo.
2.38 La lancha de la figura se va moviendo a 20 pie/s cuando su motor se apaga. Debido ala resistencia aerodinámica, su aceleración es a = -0.1 v2 pie/s2. ¿Cuál es la velocidad de la lancha 2 s después?

2.39 En el Prob. 2.38, ¿qué distancia recorre la lancha en 2 s después de que se apaga el motor?
2.40 Una bola de acero se libera del reposo en un recipiente de acero. Su aceleración hacia abajo es a = 0.9g - CV, donde g es la aceleración debida a la gravedad al nivel del mar y c es una constante. ¿Cuál es la velocidad de la bola en función del tiempo?

2.41 En el Prob. 2.40, determine la posición de la bola respecto a su posición inicial en función del tiempo.
2.42 La mayor profundidad oceánica descubierta hasta ahora se halla en las islas Marianas, en el Océano Pacífico occidental. Una bola de acero que se libere en la superficie requiere 64 minutos para llegar al fondo. La aceleración de la bola hacia abajo es a = 0.9g - cv, donde g es la aceleración debida a la gravedad al nivel del mar y la constante c=3.02 s-1.
¿Cuál es la profundidad en millas?
2.43 Para estudiar los efectos de los impactos de meteoros sobre los satélites, se usa un cañón que acelera una bola de plástico a una alta velocidad. Se determina que cuando la bola ha recorrido 1 m su velocidad es de 2.25 km/s y cuando ha recorrido 2 m, su velocidad es de 1.00 km/s. Suponga que la aceleración de la bola cuando sale del cañón está dada por a = -cv2, donde c es una constante.
(a) ¿Cuál es el valor de c y cuáles son sus unidades SI?
(b) ¿Cuál es la velocidad de la bola al salir del cañón?

2.44 Si se toma en cuenta la resistencia aerodinámica, la ace-leración de un cuerpo al caer se puede aproximar con a = g - cv2, donde g es la aceleración debida a la gravedad al nivel del mar y c es una constante.
(a) Si un cuerpo se libera del reposo, ¿cuál es su velocidad en función de la distancia s desde el punto en que se libera?
(b) Determine el límite de su respuesta a la parte (a) cuando c -> 0, y demuestre que concuerda con la solución que se obtiene al suponer su aceleración es aproximadamente a = g.
2.45 Un paracaidista salta de un helicóptero y va cayendo en línea recta a 30 m/s cuando se abre su paracaídas. A partir de ese momento su aceleración es aproximadamente a = g - cv2, donde g = 9.81 m/s2 y c es una constante. Después de un periodo inicial de “transición”, desciende a una velocidad de 5 m/s casi constante.
(a) ¿Cuál es el valor de c y cuáles son sus unidades SI?
(b) ¿A qué desaceleración máxima está sometido?
(c) ¿Cuál es su velocidad cuando ha caído 2 m desde el punto en que se abre su paracaídas?

2.46 Un trineo de retroimpulso parte del reposo y acelera con a = 3t2m/s2 hasta que su velocidad es de 1000 m/s. En ese momento encuentra un freno de agua y su aceleración es a = - 0.001v2 hasta que su velocidad disminuye a 500 m/s.
¿Qué distancia total recorre el trineo?

2.47 La velocidad de un punto está dada por la ecuación v = (24 - 2s2)1/2 m/s.
¿Cuál es su aceleración cuando s = 2 m?
2.48 La velocidad de un cuerpo sometido al campo gravitatorio de la Tierra está dada por

donde vo es la velocidad en la posición so, y RE es el radio de la Tierra. Usando esta ecuación, demuestre que la aceleración del cuerpo es a = gRE2/s2.
2.49 El análisis del movimiento de un mecanismo indica que la velocidad de un punto de conexión está dada por v= A + 4s2 pie/s, donde A es una constante. Cuando s = 2 pies, su aceleración es a = 320 pie/s2. ¿Cuál es su velocidad cuando s = 2 pies?
2.50 La aceleración de un cuerpo está dada por la función a = 2s pie/s2. Cuando t = 0, u = 1 pie/s. Halle la velocidad cuando el cuerpo se ha movido 2 pie de su posición inicial.
2.51 La aceleración de un cuerpo está dada por a = 3s2 pie/s2. En s = 0, su velocidad es v = 10 pie/s.
¿Cuál es su velocidad cuando s = 4 pie?
2.52 La velocidad de un cuerpo está dada por v2 = k/s, donde k es una constante. Si v= 4 m/s y s = 4 m en t = 0, determine la constante k y la velocidad en t = 2 s.
2.53 Un oscilador consiste en una masa y un resorte conectados como se muestra. La coordenada s mide el desplazamiento de la masa respecto a su posición cuando el resorte no está estirado. Si el resorte es lineal, la masa está sometida a una desaceleración proporcional a s. Suponga que a = -4s m/s2 y que la masa tiene una velocidad v= 1 m/s en la posición s = 0.
(a) ¿Qué distancia se moverá la masa hacia la derecha antes de que el resorte la detenga?
(b) ¿Qué velocidad tendrá la masa cuando regrese a la posición s= O?

2.54 En el Prob. 2.53 suponga que en t = 0 la masa se libera desde el reposo en la posición s = 1 m. Determine la velocidad de la masa en función de s al moverse de su posición inicial a s = 0.
2.55 En el Prob. 2.53 suponga que en t = 0 la masa se libera desde el reposo en la posición s = 1 m. Determine la posición de la masa en función del tiempo al moverse de su posición ini-cial a s = 0.
2.56 Si una nave espacial está a 100 mi sobre la superficie de la Tierra, ¿qué velocidad inicial vo requeriría para alcanzar la órbita de la Luna, a 238 000 mi del centro de la Tierra? El radio de la Tierra es de 3960 mi. Ignore el efecto de la gravedad de la Luna.

2.57 El radio de la Luna es RL= 1738 km. La aceleración de la gravedad en su superficie es 1.62 m/s2. Si un cuerpo se libera desde el reposo a 1738 km sobre la superficie de la Luna, ¿cuál es la magnitud de su velocidad justo antes de chocar con la superficie?
2.58 Usando los datos del Prob. 2.57, determine la velocidad de escape desde la superficie de la Luna.
2.59 Suponga que se puede taladrar un túnel recto a través de la Tierra, del polo norte al polo sur, y evacuar el aire. Un cuerpo liberado desde la superficie caería con aceleración a = -gs/RE, donde g es la aceleración de la gravedad al nivel del mar, RE es el radio de la Tierra y s es la distancia del cuerpo respecto al centro de la Tierra. (La aceleración gravitatoria es igual a cero en el centro de la Tierra y se incrementa linealmente con la distancia desde el centro.)
¿Cuál es la magnitud de la velocidad del cuerpo cuando éste alcanza el centro de la Tierra?

2.60 La aceleración de la gravedad de un planeta hipotético bidimensional dependería de la distancia s desde el centro del planeta según la relación a = - k/s, donde k es una constante. Sea RE, el radio del planeta y gE la magnitud de la aceleración debida a la gravedad en su superficie.
(a) Si a un cuerpo se le da una velocidad inicial vo, hacia afuera a una distancia so, desde el centro del planeta, determine su velocidad en función de s.
(b) Demuestre que no existe velocidad de escape desde un planeta bidimensional (lo cual explicaría por qué no nos han visitado seres bidimensionales).

2.61 Las coordenadas cartesianas de un punto (en metros) son x = 2t + 4, y = t3 - 2t, z = 4t2 - 4, donde t está en segun-dos.
¿Cuáles son su velocidad y su aceleración en t = 4 s?
Estrategia: Como las coordenadas cartesianas están dadas en función del tiempo, determinar las componentes de la velocidad en función del tiempo, y las componentes de la aceleración en función del tiempo.
2.62 La velocidad de un punto es v = 2i + 3t2j (pie/s). En t = 0 su posición es r = -i + 2j (pie). Halle r en t = 2 s.
2.63 Las componentes de la aceleración de un punto (en pie/s2) son ax = 3t2, ay = 6t y az = 0. En t = 0, x = 5 pie, vx = 3 pie/s, y = 1 pie, vy = -2 pie/s, z = 0 y vz = 0.
¿Cuáles son sus vectores de posición y de velocidad en t = 3 s?
2.64 Las componentes de la aceleración de un cuerpo (m/svx) son ax= 2t, ay = 4t2 - 2 y az = -6. En t = 0 la posición del cuerpo es r = 1Oj - 10k (m) y su velocidad es v = 2i - 4j (m/s).
Determine su posición cuando t = 4 s.
2.65 Se diseña un mortero para lanzar una cuerda de salvamento desde un guardacostas a un buque en zozobra. La cuerda está unida a un peso que es lanzado por el mortero. El mortero se montará en forma tal que disparará a 45o sobre la horizontal. Si se ignoran la resistencia del aire y el peso de la cuerda en el diseño preliminar, y se supone una velocidad inicial en la boca del mortero de 100 pie/s en t = 0, Lcuáles son las coordenadas x y y del peso en función del tiempo?

2.66 En el Prob. 2.65, Lcuál debe ser la velocidad en la salida del mortero para alcanzar barcos a una distancia de 1000 pies? 2.67 Si se lanza horizontalmente una piedra desde la azotea de un edificio de 100 pies de altura a 50 pie/s, ¿a qué distancia horizontal desde el punto en que se lanzó tocará el suelo? (Suponga suelo a nivel.) ¿Cuál es la magnitud de su velocidad justo antes de tocar el suelo?

2.68 Un proyectil se dispara desde el nivel del suelo con velocidad inicial vo. ¿Con qué ángulo inicial qo, sobre la horizontal se logra el alcance máximo R, y qué valor tiene este alcance máximo?

2.69 Un piloto quiere lanzar suministros en cierta región remota. Pretende volar horizontalmente y soltar los paquetes sin velocidad vertical. Deduzca una ecuación para la distancia horizontal d a la que debe soltar el paquete en términos de la velocidad vo y la altura h del avión.

2.70 Un bateador golpea la pelota a 3 pies sobre el cojín de home y la eleva con un ángulo de 60º sobre la horizontal. El segunda base la toma a 6 pies sobre la segunda base. ¿Cuál fue la velocidad inicial de la pelota?

2.71 En el Prob. 2.70, ¿a qué altura sobre el campo voló la pelota?
2.72 Un pitcher lanza una bola rápida con velocidad inicial vo= 90 mi/h. Sea q el ángulo inicial del vector de velocidad de la pelota sobre la horizontal. Cuando la pelota es lanzada, está a 6 pies sobre el terreno y a 58 pies del bateador. La zona de strike del bateador (entre sus rodillas y sus hombros) se extiende entre 1 pie 10 pulg sobre el terreno y 4 pies 6 pulg. Ignorando efectos aerodinámicos, determine si la pelota pasará por la zona de strike:
(a) si q= lº; (b) si q= 2º.

2.73 En el Prob. 2.72 suponga que elpitcher lanza la pelota con un ángulo q= 1º sobre la horizontal y determine el intervalo de velocidades vo (en pie/s) con que debe lanzar la pelota para que ésta pase por la zona de strike.
2.74 Un zoólogo está provisto de un arco y una flecha que tiene una jeringa con tranquilizador, pues debe medir la temperatura de un rinoceronte. El alcance máximo es de 100 m. Si el rinoceronte embiste directamente hacia el zoólogo a 30 km/h y éste apunta su arco 20º sobre la horizontal, ¿a qué distancia debe estar el rinoceronte cuando dispare la flecha?

2.75 Los clavadistas de La Quebrada en Acapulco deben sin cronizar sus clavados de modo que entren al agua en la cresta de una ola. Las crestas de las olas tienen 2 pies sobre la profundidad media h = 12 pies del agua; la velocidad de las olas es raíz cuadrada de gh. La meta de los clavadistas es un punto a 6 pies de la base del acantilado. Suponga que cuando se inicia el clavado la velocidad es horizontal.
(a) ¿Cuál es la magnitud de la velocidad en mi/h cuando entran al agua?
(b) ¿A qué distancia de la meta debe estar la cresta de la ola cuando se lanza un clavadista para que entre al agua sobre ella?

2.76 Un proyectil se lanza a 10 m/s desde una superficie inclinada. Determine el alcance R.

2.77 Un esquiador salta de una pendiente de 20º a 50 pie/s.
(a) Determine la distancia d al punto en que cae.
(b) Determine las componentes de su velocidad paralela y perpendicular a la pendiente de 45º cuando cae.

2.78 A una bola de acero en un tanque de aceite se le da, en t = 0, una velocidad horizontal v = 2i m/s. Las componentes de su aceleración en m/s2 son ax, = -1.2 vx, ay = -8 - 1.2 vy, az = -1.2 vz. ¿Cuál es la velocidad de la bola en t = 1 s?

2.79 En el Prob. 2.78, ¿cuál es la posición de la bola en t = 1 s respecto a su posición en t = 0?
2.80 Se debe diseñar un dispositivo para una línea de ensamblaje que lance pequeñas piezas al aire, las cuales caerán en un recipiente. El punto de lanzamiento es x= 200 mm, y= -50 mm, z = -100 mm (el eje y es vertical y positivo hacia arriba). Para caer en el recipiente, las piezas deben pasar por el punto x = 600mm,y = 200mm,z = -100mm moviéndose horizontalmente. Determine las componentes de la velocidad que el lanzador debe dar a las piezas.
2.81. Si y=150 mm, dy/dt=300 mm/s y d2y/dt2=0, ¿cuáles son las magnitudes de la velocidad y la aceleración del punto P?

2.82 Un automóvil viaja a 100 km/h sobre un camino recto con pendiente creciente cuyo perfil vertical se puede aproximar con la ecuación mostrada. Cuando la coordenada horizontal del automóvil es x = 400 m, ¿cuál es su aceleración?

2.83 Suponga que un proyectil tiene las condiciones iniciales mostradas en la siguiente figura:

. Demuestre que en el sistema coordenado x’y’ con su origen en el punto más alto de la trayectoria, la ecuación que describe a ésta es

2.84 Las componentes de la aceleración de un punto son ax = -4 cos qt, ay = -4 sen qt, az = 0. En t = 0 su posición y velocidad son r = i, v = 2j. Demuestre que:
(a) la magnitud de la velocidad es constante;
(b) los vectores de velocidad y de aceleración son perpendiculares;
(c) la magnitud de la aceleración es constante y señala hacia el origen;
(d) la trayectoria del punto es un círculo con su centro en el origen.
Pag.49.ALS
Hemos visto que en algunos casos el movimiento curvilíneo de un punto se puede analizar usando coordenadas cartesianas. En las siguientes sec-ciones describimos problemas que se pueden analizar más fácilmente con otros sistemas coordenados. En esta sección presentamos dos temas preli-minares: el movimiento angular de una línea en un plano y la derivada respecto al tiempo de un vector unitario girando en un plano.
Movimiento angular de una línea Podemos especificar la posición angular de una línea L en un plano particular respecto a una línea de refe-rencia L, en el plano por medio del ángulo q (Fig. 2.18). La velocidad angular de L respecto a Lo, está definida por w=dq/dt (2.31) Figura 2.18 Línea L y línea de referencia L,, en un plano.
2.96 La armadura de un motor eléctrico gira a razón constante. La magnitud de la velocidad del punto P respecto a 0 es 4 m/s.
(a) ¿Cuáles son las componentes normal y tangencial de la aceleración de P respecto a O?
(b) ¿Cuál es la velocidad angular de la armadura?
2.97 La armadura del Prob. 2.96 parte del reposo y tiene una aceleración angular constante a= 10 rad/s2. ¿Cuál es la velocidad y la aceleración de P respecto a 0 en términos de las componentes radial y tangencial después de 10 s?
2.98 Las centrífugas se usan en los laboratorios médicos para aumentar la velocidad de precipitación de la materia sólida presente en soluciones. Suponga que se quiere diseñar una centrífuga para someter muestras a aceleraciones de 1000 g.
(a) Si la distancia del centro de la centrífuga a la muestra es de 300 mm, ¿qué velocidad de rotación en rpm se necesita?
(b) Si se quiere que la centrífuga alcance sus rpm de diseño en 1 min , ¿qué aceleración angular constante se necesita?
yELtml~ P2.98 P2.99
2.99 Una lancha de motor parte del reposo y es conducida en una trayectoria circular de 40 pies de radio. La magnitud de su velocidad aumenta a una razón constante de 2 pie/s2. En términos de las componentes normal y tangencial, determine:
a)la velocidad en función del tiempo
(b)la aceleración en función del tiempo.
2.100 Se tiene el ángulo q= 2t2 rad.
(a) ¿Cuál es la magnitud de la velocidad y de la aceleración de P respecto a 0 en t = 1 s?
(b) ¿Qué distancia a lo largo de la trayectoria circular recorre P entre t = 0 y t = 1 s?
2.101 En el Prob. 2.100, icuál es la magnitud de la velocidad y de la aceleración de P respecto a 0 cuando P ha efectuado una revolución en la trayectoria circular comenzando en t = O?
2.102 El radio de la Tierra es de 3960 millas. Si usted está de pie en el ecuador, ¿cuál es la magnitud de su velocidad respecto al centro de la Tierra?
2.103 El radio de la Tierra es de 6370 km. Si usted está de pie en el ecuador, ¿cuál es la magnitud de su aceleración respecto al centro de la Tierra?
2.104 Suponga que usted está de pie en un punto P a 30” de latitud norte (es decir, en un punto a 30” al norte del ecuador). El radio de la Tierra es R, = 3960 millas.¿Cuáles son las magnitudes de su velocidad y aceleración respecto al centro de la Tierra?
2.105 La magnitud de la velocidad del avión mostrado es constante e igual a 400 m/s. La razón de cambio del ángulo 0 de su trayectoria es constante e igual a 5”/s.
(a) ¿Cuáles son la velocidad y la aceleración del avión en términos de componentes normal y tangencial?
(b) ¿Cuál es el radio de curvatura instantáneo de la trayectoria del avión?
2.106 En t = 0, un automóvil parte del reposo en el punto A. Se mueve hacia la derecha y la componente tangencial de su aceleración es a, = 0.4t m/s2. ¿Cuál es la magnitud de la aceleración del automóvil cuando llega al punto B?
2.107 Un automóvil incrementa su velocidad a una razón constante de 40 mi/h en A a 60 mi/h en B.¿Cuál es la magnitud de su aceleración 2 s después de que pasa por el punto A?
2.108 Determine la magnitud de la aceleración del automóvil P2.104 del Prob. 2.107 cuando ha viajado a lo largo del camino una distancia:
(a) de 120 pies desde A
(b) de 160 pies desde 4.
2.109 Un aspirante a astronauta va a someterse a una prueba en una centrífuga con radio de 10 m. El perderá la conciencia si su aceleración horizontal total llega a 14 g. ¿Cuál debe ser la aceleración angular constante máxima de la centrífuga, partiendo de cero, para que esta persona no pierda la conciencia en el primer minuto?
2.110
Suponga que un sistema bloque-resorte tiene k=18 N/m, y m=0.71kg y que el sistema oscila con una amplitud A= 54 mm.Determinar:
a) La frecuencia angular de las oscilaciones.
b) Obtenga una expresión para la separación entre el bloque y la posición central |x| en función de la velocidad v, y utilice esta expresión para encontrar |x| cuando v=0.18m/s
135876
